Hello world !
This week we are solving the last (and final) practice round of Google’s 2013 kickstart edition.
Problem Statement

In a league of evil villains, there has been trouble amongst the members. Their leader, Bad Horse, has taken it upon him to bring back peace. He knows which of his members don’t get along. As such, he would like to know whether they could be split up in two different (peaceful) groups for future get-togethers.
Bad Horse isn’t that smart, so he needs you to solve the problem…
Constraints
Input
The first line of the input gives the number of test cases, T. T lines follow. Each test case start with a positive integer M on a line by itself, followed by M pairs of troublesome villains (one pair per line, separated by spaces.)
Output
For each test case, the output should be Case #x: y, where x is the case number (starting from one) and y is the answer (Yes / No).
Sample

Solving the problem
The problem is quite simple: we need to use the given pairs of villains to determine whether they can be split up in two groups that do not contain one of the given pairs.
A very straightforward approach would consist of “brute-forcing” the solution by trying all possible group combinations (through backtracking for instance) and returning whether 2 groups that satisfy such condition exist. One would agree this process might be long and computationally expensive.
Whenever I am confronted to such problems, I ask myself the question: “What are simple examples that yield {insert positive outcome here} and example that yield {insert negative outcome here}. Luckily, Google provides us with 2 test cases.
Visual Representation
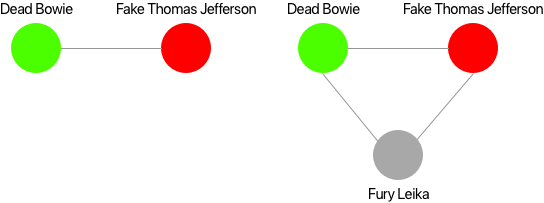
We can represent this network of villains as a graph and assign them a color that represents their respective groups:
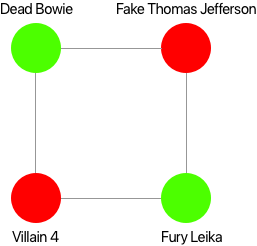
The first example is really obvious. The second example is very useful: it indicates that the presence of a cycle would make the partitioning fail. However, if one villain was to be added to this cycle, the partitioning would be able to succeed again:
Hence, we can extract the key information that the presence of an odd-length cycle makes a bipartition impossible.
Mathematical foundations
Bad Horse’s problem is what is commonly known as the graph bipartition problem. It aims to determine whether a graph can be divided in two groups of nodes of which none are adjacent. If such division is possible, the graph is called bipartite.
Finding an answer to that problem consists of finding out whether the graph contains an odd-length cycle. If it doesn’t, the graph is bipartite. Easier said than done! Finding all cycles contained within a very big graph can be a long and complex process.
Luckily, the problem can be translated to something more simplistic called the two-coloring problem. Here, we ask the question if a given graph (network of villains) can be colored using only two colors. The only rule that must be satisfied is that adjacent nodes cannot share the same color.
Implementing a two-coloring problem
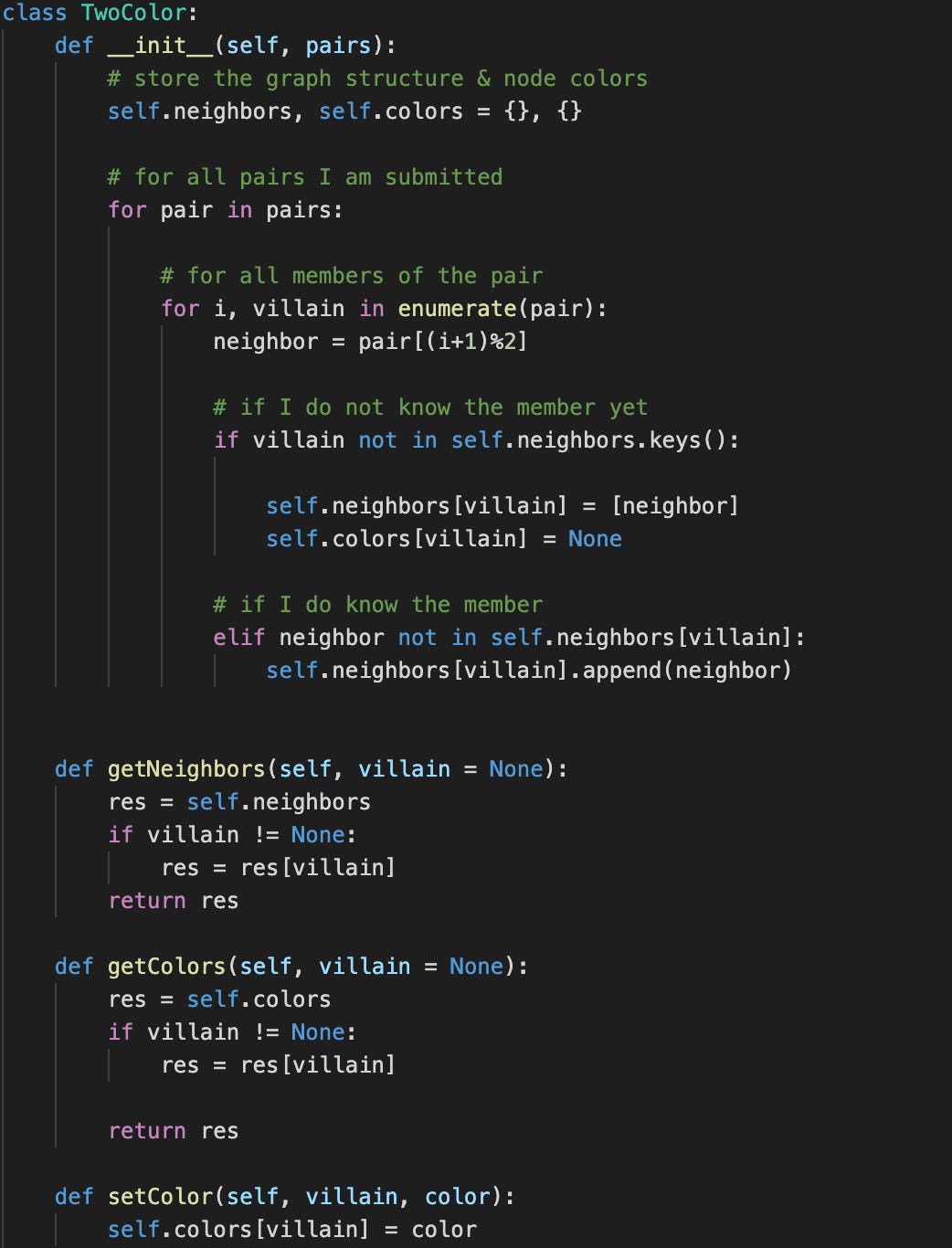
The first challenge is to be able to take Google’s input and translate that into Python variables. I decided to store all pairs in lists (1 list = 1 pair) and store all of these into one global list.
The list is then fed to the TwoColor object, that will determine whether the described network is indeed bipartite.
Next, we want to transform these pairs into a usable structure. During the initialization of TwoColor, two dictionaries are built: a neighbors dictionary that contains all the neighbors of each villain (the graph), and color dictionary that contains the color of each villain.
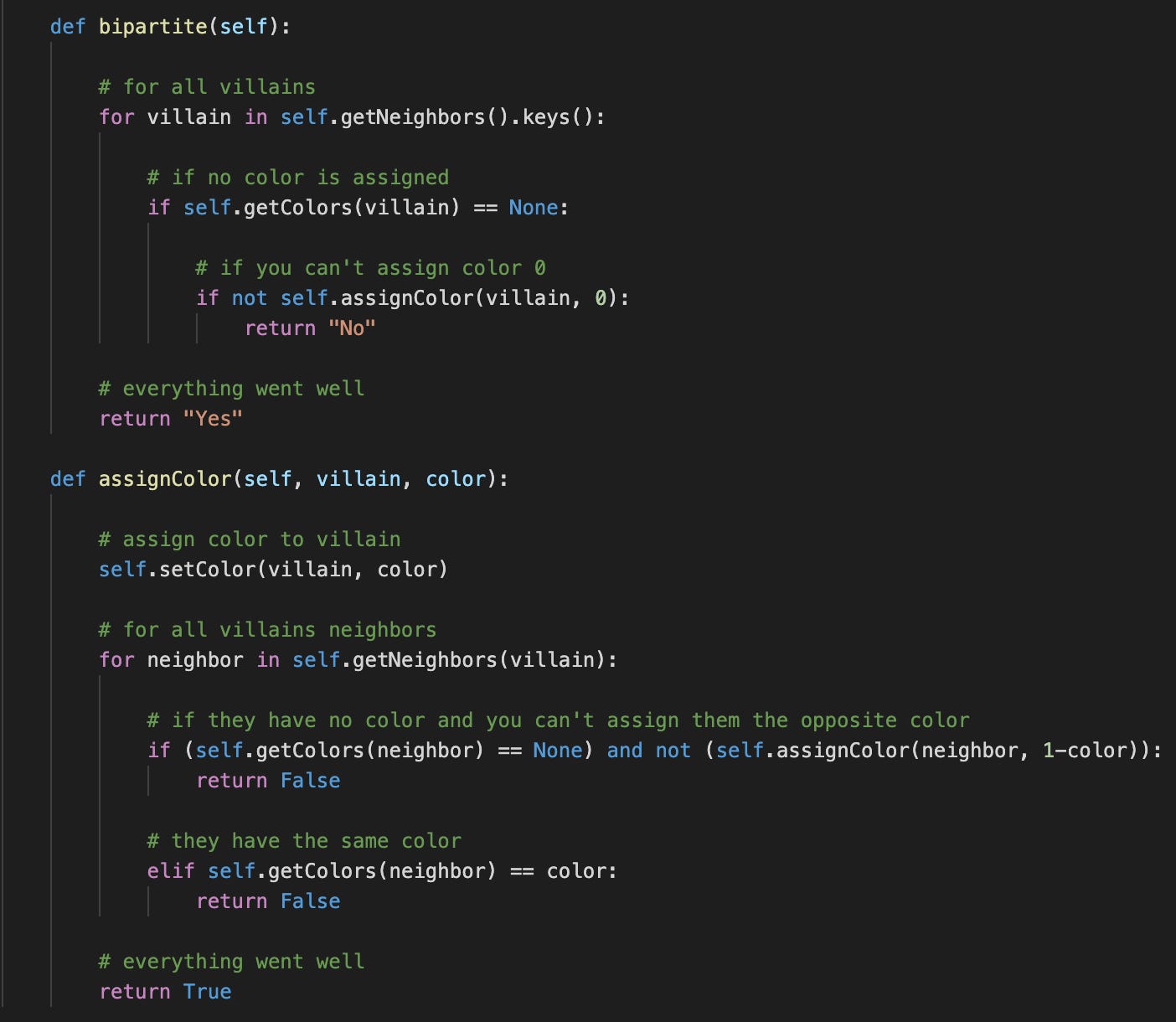
Now, we can move on to solving the problem. The logic is extremely straightforward: for every node, we want to assign it a color (if it has none) and then verify that no neighbor has the same color and all neighbors are / can be colored in the opposite color.
As you might have noticed, this is a perfect example of recursion: the condition is only satisfied if all neighbors of each node can be colored that way.
The code literally translates this into these two methods: if the color 0 can’t be assigned to the first villain, the bipartition fails. Assigning a color simply consists of updating our color dictionary and verifying that:
No neighbor has the same color
No neighbors without color can’t be assigned the opposite color
In other words: all neighbors either have the opposite color, or can be assigned the opposite color. For each neighbor, the code will apply this same logic in a recursive fashion.
Now Bad Horse a happy villain!
*Wacky Coder out*